XGBoost, short for eXtreme Gradient Boosting, is a powerful and commonly used algorithm, highly renowned for its accuracy and speed in predictive modeling across various domains like industry competitions, finance, insurance, and healthcare.

How XGBoost Works

XGBoost builds a series of trees to make predictions, and each tree corrects errors made by the previous ones. The algorithm minimizes a loss function, often the mean squared error for regression tasks and the log loss for classification tasks.

The ensemble of trees in XGBoost is more flexible and capable than traditional gradient boosting due to:

• Regularization: This controls model complexity to prevent overfitting, contributing to XGBoost’s robustness.
• Shrinkage: Each tree’s contribution is modulated, reducing the impact of outliers.
• Cross-Validation: XGBoost internally performs cross-validation tasks to fine-tune hyperparameters, such as the number of trees, boosting round, etc.

Key Features of XGBoost

1. Parallel Processing: The advanced model construction techniques, including parallel and distributed computing, deliver high efficiency.

2. Feature Importance: XGBoost offers insightful mechanisms to rank and select features, empowering better decision-making.

3. Handling Missing Data: It can manage missing data in both the training and evaluation phases, simplifying real-world data scenarios.

4. Flexibility: XGBoost effectively addresses diverse situations like classification, regression, and ranking.

5. GPU Support: It optionally taps into GPU’s immense parallel processing capabilities, further expediting computations.

Python: Code Example for XGBoost Model

Here is the Python code:

import xgboost as xgb
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# Load Boston dataset
boston = load_boston()
X, y = boston.data, boston.target

# Train-test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Build XGBoost model
xg_reg = xgb.XGBRegressor(objective ='reg:squarederror', colsample_bytree = 0.3, learning_rate = 0.1, max_depth = 5, alpha = 10, n_estimators = 10)
xg_reg.fit(X_train, y_train)

# Predict and evaluate the model
preds = xg_reg.predict(X_test)
rmse = mean_squared_error(y_test, preds, squared=False)
print("RMSE: %f" % (rmse))

XGBoost is a highly optimized implementation of gradient boosted trees designed for both efficiency and better performance. Let’s explore the key differences between XGBoost and GBM.

Tree Construction

• XGBoost: Trees are built level-wise, which can sometimes sacrifice detailed local adjustments but often speeds up the building process and brings better overall performance.

• GBM: Trees are commonly built using a leaf-wise strategy, potentially leading to more refined models for regions with many observations.

Regularization Techniques

• XGBoost: It employs both L1 (LASSO) and L2 (Ridge Regression) regularizations, enhancing generalization and combating overfitting.

• GBM: While conventional implementations permit only L2 regularization, newer versions may also support L1.

Parallelism

• XGBoost: Offers parallelism for tree construction, node splitting, and column selection.

• GBM: Some libraries do support multi-threading, but for the most part, tree building is sequential.

Missing Data Handling

• XGBoost: It automatically determines the best path for missing values during training.

• GBM: Missing data handling usually requires explicit handling and definition at the user’s end.

Algorithm Complexity

• XGBoost: Optimization techniques like column block structures, sparse-aware data representation, and out-of-core computing make it computationally efficient.

• GBM: Although conceptually simpler, its lack of specialized techniques might make it less efficient for certain datasets.

Split Finding Techniques

• XGBoost: Employs the exact or approximate greedy algorithm for split discovery.

• GBM: Conventionally utilizes the greedy algorithm.

Custom Loss and Evaluation Metrics

• XGBoost: Users can define custom objective and evaluation metrics for specific tasks.

• GBM: Supports only the predefined objective and evaluation metrics.

Code Example: Training a Simple Model Using XGBoost

Here is the code:

import xgboost as xgb
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# Load the Boston housing dataset
boston = load_boston()
X, y = boston.data, boston.target

# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Convert the dataset to DMatrix
data_dmatrix = xgb.DMatrix(data=X, label=y)

# Instantiate and train the XGBoost model
xg_reg = xgb.XGBRegressor(objective ='reg:squarederror', colsample_bytree = 0.3, learning_rate = 0.1,
                max_depth = 5, alpha = 10, n_estimators = 100)
xg_reg.fit(X_train, y_train)

# Make predictions and evaluate the model
preds = xg_reg.predict(X_test)
rmse = mean_squared_error(y_test, preds, squared=False)
print("RMSE: %.2f" % (rmse))

XGBoost has built-in mechanisms to effectively handle missing or null values. This powerful feature makes it ideal for datasets with incomplete information.

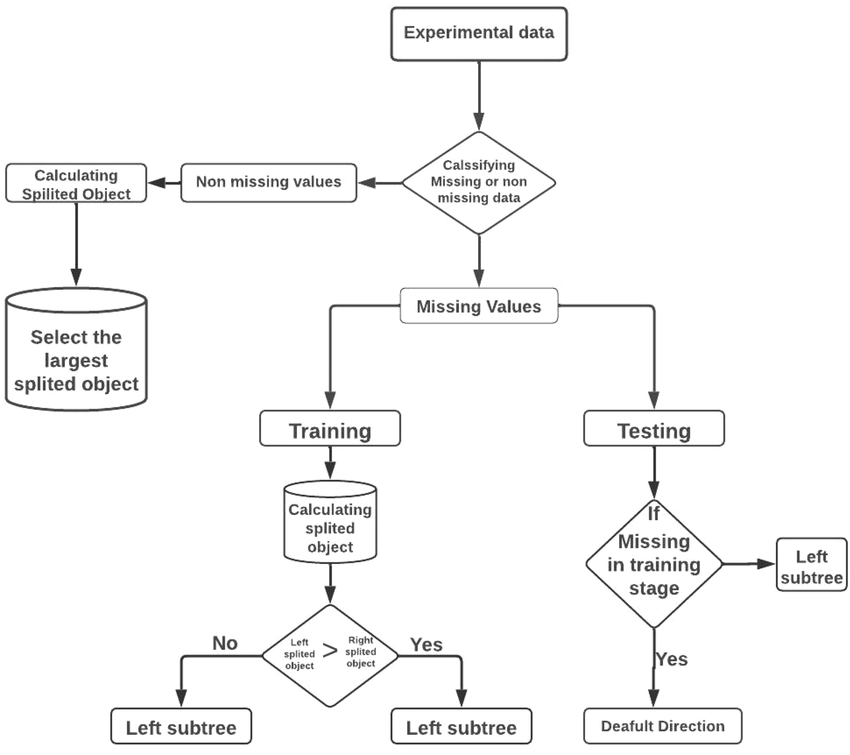
Sparsity-Aware Split Finding

XGBoost automatically detects if a feature is missing and learns the best direction to move in the tree to minimize loss. The algorithm makes this decision during split finding and tree building. If a missing value does not help improve the loss, the path leading to this missing value is minimized by setting the associated weights to 0.

Weight Adjustments

The algorithm utilizes three-to-five splits, depending on the best solution. If a feature is missing, weights of leaf nodes with missing values are adjusted.

Visual Representation: Handling Missing Data

Code Example: Utilizing xgboost.DMatrix

In the Python code provided, xgboost.DMatrix is used for more fine-grained control.

import xgboost as xgb
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split

# Creating a sample dataset with missing values
data = {
    'feature1': [1, 2, np.nan, 4, 5],
    'label': [0, 1, 0, 1, 0]
}
df = pd.DataFrame(data)

# Assigning missing values to a column
df.loc[df['feature1'].isnull(), 'feature1'] = -999

# Splitting the dataset
X_train, X_test, y_train, y_test = train_test_split(df['feature1'], df['label'], test_size=0.2)

# Converting the dataset to 'DMatrix'
dtrain = xgb.DMatrix(X_train, label=y_train)
dtest = xgb.DMatrix(X_test, label=y_test)

# Defining model parameters
params = {
    'objective': 'binary:logistic',
    'eval_metric': 'logloss'
}

# Training the model
model = xgb.train(params, dtrain, num_boost_round=10)

# Making predictions
preds = model.predict(dtest)

Here, we’re allowing the model to consider -999 as a representation for missing data.

Regularization in XGBoost is a technique used to prevent overfitting by adding a penalty term to the model’s objective function. This term discourages overly complex models and is there to ensure that the tree does rely solely on the most prominent features.

Regularization Parameters in XGBoost

XGBoost offers several hyperparameters for controlling the regularization strength:

1. L1 Regularization (alpha or reg_alpha): Encourages sparsity in feature selection by adding the sum of absolute values of the weights to the cost function.

   $$J = J_0 + \alpha \sum_{i=1}^n |w_i|$$

2. L2 Regularization (lambda or reg_lambda or reg_weight): Also known as weight decay, it adds the sum of squares of the weights to the cost function.

   $$J = J_0 + \lambda \frac{1}{2} \sum_{i=1}^n w_i^2$$

3. Max Depth (max_depth): Another form of regularization, it limits the maximum depth a tree can grow to.

4. Minimum Child Weight (min_child_weight): This parameter also assists in controlling leaf node size, thereby preventing splitting in specific cases when a leaf is too weighted.

XGBoost (Extreme Gradient Boosting) and Random Forests are both powerful ensemble learning techniques, but they employ distinct methodologies.

Key Differences

Boosting vs. Bagging

• XGBoost: Utilizes a boosting approach that iteratively builds trees to address the shortcomings of preceding ones.

• Random Forests: Operates on a bagging strategy that constructs trees independently, and the ensemble averages their predictions.

Tree Building Mechanism

• XGBoost: Employs a learning algorithm that incorporates

  • Early stopping
  • Regularization techniques such as $L1$ (LASSO) and $L2$ (ridge) to minimize overfitting.
  • Computational efficiency via split finding algorithms using approximate tree boosting.

• Random Forests: Uses feature randomness and bootstrapping (sampling with replacement) to build multiple trees. Each tree considers a random subset of features at each split.

XGBoost Add-Ons

• Bias and Variance Reduction: XGBoost offers better control over bias-variance tradeoff, allowing users to steer the model into a higher bias or variance regime according to their datasets and objectives.
• Cross-Validation Integration: The library can embed cross-validation during the model’s training process, making it more adaptable to varying dataset characteristics.
• Integrated Shrinkage: Unified approach to shrinkage capabilities via “learning rate,” which can contribute to model generalization and speed.

Verification Efficiency

• XGBoost: Verification occurs on the most recent tree after each iteration, enhancing the process’s efficiency.
• Random Forests: Inspects all the trees, leading to a relatively slower operation.

Computational Efficiency

• XGBoost: Leverages multiple threads and directs core utilization for parameter tuning and constructing decision trees, granting it a computational advantage.
• Random Forests: Although computationally robust, its performance can reduce in high-dimensional settings when faced with an extensive list of input features.

Outlier Handling

• XGBoost: Can be sensitive to extreme data points or outliers in certain scenarios.
• Random Forests: With the ensemble averaging method, Random Forests are frequently more impervious to outliers.

Parallel Processing

• XGBoost: Implies a parallel computational structure for tree construction, while in Random Forests, such an arrangement might be constrained to bootstrapping.
• Random Forests: Limited parallelism due to the bootstrapping-based strategy for tree construction.

Gradient Boosted Models (GBMs) are ensemble methods that build models in a forward stepwise manner, using decision trees as base learners. The algorithm can be computationally intensive, making it a somewhat challenging learning model. However, through its improved accuracy and speed, along with advanced regularization techniques, it’s still a popular option.

Extreme Gradient Boosting (XGBoost) is a variant of this algorithm optimized for both speed and performance, offering several unique features.

Key Concepts and Methodology

• Sequential Training: XGBoost uses an approach called boosting, where each new model targets errors from the prior ones, creating an additive sequence of predictors.

• Gradient Optimization: The algorithm minimizes a predefined loss function by following the steepest descent in the model’s parameter space.

• Principle Components: Boosting iteratively fits small, simple models to the residuals of the preceding model, refining these fits over time and, in turn, improving the overall prediction.

• Shrinkage (Learning Rate): Learning rate, typically small (e.g., 0.1), scales the contribution of each tree. Lower learning rates yield better accuracy at the cost of slower convergence.

• Tree Pruning: The trees can be pruned of their most irrelevant subtrees, which both boosts efficiency and limits overfitting.

• Regularization: Both L1 and L2 regularization are used, reducing the risk of overfitting.

• Feature Importance: The model calculates the importance of each feature, aiding in the selection process.

• Support for Missing Data: The models natively handle missing data.

• Cross-Validation: A built-in function for cross-validation helps choose the optimal number of trees.

XGBoost Enhancements

XGBoost has a set of features that make it faster and more effective than traditional GBMs:

• Algorithmic Enhancements: Several techniques, like approximate tree learning, enhance efficiency without compromising accuracy.

• Hardware Optimization: Multi-threading and selective GPU support improves speed and performance.

• Built-in Cross-Validation: Its algorithms include an efficient method for cross-validation, significantly simplifying the validation process.

• Integrated Regularization: The model automatically applies L1 and L2 regularization.

• Monotonicity Constraints: XGBoost lets you specify whether the model should have a positive or negative relationship with each feature, implementing business logic into the model.

XGBoost offers various performance measure approaches, known as loss functions, to optimize model training for regression and classification tasks.

Regression Loss Functions

1. Squared Loss (L2 Loss): Primarily used for mean target estimation in regression tasks. It measures the difference between predicted and actual values, summing up the squared differences across all instances. L2 regularization adds a penalty term based on the sum of squared model weights.

   $$L = \frac{1}{2} \sum_{i=1}^{n} (y_i - \hat{y}$$i)^2 + \alpha \sum{j=1}^{k} \omega_j^2

2. Absolute Loss (L1 Loss): This loss function uses the absolute difference between the predicted and actual values instead of squares.

   $$L = \sum_{i=1}^{n} |y_i - \hat{y}$$i| + \alpha \sum{j=1}^{k} |\omega_j|

3. Huber Loss: A combination of L1 and L2 Loss that is less sensitive to outliers. It switches to L1 Loss if the absolute difference is above a $\delta$ threshold.

   def huber_loss(y_true, y_predicted, delta):
       error = y_true - y_predicted
       return np.where(np.abs(error) < delta, 0.5 * error**2, delta * (np.abs(error) - 0.5 * delta))
   

Classification Loss Functions

1. Logistic Loss: Commonly employed in binary classification problems. It calculates the likelihood of the predicted class, converting it to a probability with a sigmoid function.

   $$L = -\sum_{i=1}^{n} \left[ y_i \log p_i + (1 - y_i) \log (1 - p_i) \right]$$

2. Softmax Loss: Generally used for multi-class classification tasks. It calculates a probability distribution for each class and maximizes the likelihood across all classes.

   $$L = -\sum_{i=1}^{n} \sum_{j=1}^{k} y_{ij} \log(p_{ij})$$

3. Adaptive Log Loss (ALogLoss): Introduced in XGBoost, this loss function provides a balance between speed and accuracy. It’s derived by approximating the Poisson likelihood.

XGBoost is a powerful and efficient ensemble learning model that uses a collection of weak predictive models, often decision trees, to create a strong learner.

Central to XGBoost’s effectiveness is its implementation of tree pruning, which optimizes each decision tree for enhanced overall model performance.

Role of Tree Pruning in Decision Trees

Traditional decision trees can grow too large and complex, leading to patterns that are unique to the training data, a phenomenon referred to as overfitting.

• Overfitting: Trees become excessively detailed, capturing noise in the training data and failing to generalize well to unseen data.

To mitigate overfitting, XGBoost incorporates tree pruning, a process involving tree reduction based on optimizing for limited tree depth and node purity, where purity measures how well a node separates classes or predicts a continuous value.

Techniques for Tree Pruning

• Pre-Pruning: Stops tree growth early based on user-defined hyperparameters, such as maximum depth, minimum samples per leaf, and minimum samples per split.
• Post-Pruning (Regularization): Consists of backward, bottom-up evaluations to remove or replace nodes that don’t improve a predefined splitting criterion while minimizing a regularized cost function.

These measures ensure that each component tree, or weak learner, is appropriately controlled in size and predictive characteristics.

Advantages of Pruning Techniques

1. Reduced Overfitting: Regular pruning and path shortening improve model generalization, especially for noisy or limited training data.

2. Faster Computations: Smaller trees require less time for predictions. Efficient algorithms further speed up the process.

3. Enhanced Feature Evaluation: Without excessive tree depth, it becomes easier to discern feature importance based on their splits, which can guide decision-making in real-world applications.

4. Improved Model Understanding and Interpretability: Simpler trees are easier to visualize and interpret, facilitating better comprehension for stakeholders.

Code Example: Regularize Tree Depth with XGBoost

Here is the Python code:

import xgboost as xgb
from xgboost import XGBClassifier
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split

# Load some example data
data = load_breast_cancer()
X = data.data
y = data.target

# Split to train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Creating the XGBoost model with regularized tree depth
xgb_model = XGBClassifier(max_depth=3, learning_rate=0.1, n_estimators=100)
xgb_model.fit(X_train, y_train)

# Making predictions
y_pred = xgb_model.predict(X_test)

In this example, max_depth=3 is used to control the tree depth, which can help prevent overfitting and improve computational efficiency.

Learning Rate, also known as shrinkage, refers to a technique in XGBoost that influences the contribution of each tree to the final prediction. This mechanism is designed to improve the balance between model complexity and learning speed.

Mechanism

• Each prediction step in an XGBoost model is the sum of predictions from all trees. The learning rate scales the contribution of each tree, allowing the model to require fewer trees during training.

  $$\text{Prediction}$${\text{xgboost}} = \sum{\text{Trees}}\left( \text{Learning Rate} \times \text{Individual Tree Prediction} \right)

• Post-multiplication, the shrinkage factor reduces the influence of each tree’s prediction in the final result.

Core Functions

• Regularization: Learning Rate affects the strength of the regularization methods like L1 and L2. With a smaller learning rate, the model is trained for a longer duration, potentially intensifying the impact of regularization.

• Effect on Overfitting: A lower rate implies a lower learning speed, which can mitigate overfitting.

• Speed and Convergence: A higher learning rate accelerates training but can result in oscillations around the local minimum. Meanwhile, a lower learning rate leads to steadier convergence, suitable for reaching the global minimum.

Practical Tuning Tips

• Grid Search: Allocate specific learning rate ranges in grid searches to determine the optimal value.

• Cross-Validation: Validate learning rates along with other hyperparameters using cross-validation to guarantee robust model performance.

XGBoost also offers various hyperparameters for performance optimization. Let’s explore the core ones often tuned during cross-validation and grid search.

Core Parameters

• N-estimators: The number of boosting rounds. Higher values can lead to overfitting, so it’s crucial for model stability.
• Max depth: Determines the maximum depth of each tree for better control over model complexity. Deeper trees can lead to overfitting.
• Subsample: Represents the fraction of data to be randomly sampled for each boosting round, helping to prevent overfitting.
• Learning rate (eta): Scales the contribution of each tree, offering both control over speed and potential for better accuracy.

Regularization Parameters

• Gamma (min_split_loss): Specifies the minimum loss reduction required to make a further partition.
• Alpha & Lambda: Control the L1 and L2 regularization terms, aiding in case of highly-correlated features.

Cross-Validation and Scoring

• Objective: Defines the loss function to be optimized, such as ‘reg:squarederror’ for regression and ‘binary:logistic’ for binary classification. There are various objectives catering to different problems.
• Evaluation Metric: Defines the metric to be used for cross-validation and model evaluation, such as ‘rmse’ for regression and ‘auc’ for binary classification.

Specialized Parameters

• Max delta step: Useful for those employing Logistic Regression with imbalanced classes.
• Tree method: For specifying the tree construction method like ‘hist’ for approximate tree method.
• Scale Pos Weight: For imbalanced class problems.
• Silent: Used for suppressing all messages.
• Seed: Controls the randomness.

Model Training Parameters

• Learning Rate (eta): Scales the contribution of each tree, offering both control over speed and potential for better accuracy.
• gamma (alias: min_split_loss): Specifies the minimum loss reduction required to make a further partition.
• colsample_bytree: The fraction of features to select from at each level of the tree.
• lambda (alias: reg_lambda): L2 regularization term on weights.
• alpha (alias: reg_alpha): L1 regularization term on weights.

Device and Storage Parameters

• Determining the memory constraints and speeding up training.
• CPU/GPU selection.

Advanced Parameters

• Dart: Helps avoid overfitting through aggressive dropout.
• Colsample_bynode: Controls the fraction of features to be used for each node split in a specific level.
• Categorical Features: Incorporates categorical features in XGBoost models.

APIs for Distributed Computing

• process_type and updater.

Code Example: Parameter Tuning

Here is the Python code:

import xgboost as xgb
from sklearn.datasets import load_boston
from sklearn.model_selection import GridSearchCV, train_test_split
from sklearn.metrics import mean_squared_error

# Load Boston housing data
boston = load_boston()
X, y = boston.data, boston.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Define hyperparameters for grid search
params = {
    'n_estimators': [100, 200, 300],
    'max_depth': [3, 5, 7],
    'learning_rate': [0.1, 0.01, 0.001]
}

# Instantiate and fit the model with cross-validation and grid search
xg_reg = xgb.XGBRegressor(eval_metric='rmse')
grid_search = GridSearchCV(estimator=xg_reg, param_grid=params, scoring='neg_mean_squared_error', cv=5)
grid_search.fit(X_train, y_train)

# Get best parameters and evaluate on test set
best_params = grid_search.best_params_
best_model = grid_search.best_estimator_
y_pred = best_model.predict(X_test)
rmse = mean_squared_error(y_test, y_pred, squared=False)

print("Best parameters from grid search:", best_params)
print("RMSE on test set:", rmse)

In XGBoost, the ‘max_depth’ parameter sets the maximum depth of each tree, corresponding to the number of nodes from the root to the farthest leaf. Restricting this depth enhances performance across a variety of regression and classification tasks.

Benefits of Setting ‘max_depth’

• Prevents Overfitting: A shallow tree can generalize better on unseen data, reducing overfitting risks.
• Computational Efficiency: By limiting the tree’s depth, XGBoost conserves memory use and computational resources. This efficiency is vital in handling large datasets and during real-time prediction.

Rule of Thumb

• For a binary classification task with many features, a ‘max_depth’ of 2 to 8 is often optimal.
• Utilize default values whenever possible. XGBoost’s built-in mechanisms typically lead to effective, robust models with minimal manual parameter tuning.

Balancing the learning rate (or shrinkage) and the number of boosting stages (or trees) in XGBoost is critical for optimizing both training duration and predictive accuracy.

The Trade-Off

• Learning Rate: Affects the influence of each tree on the final outcome. Smaller rates necessitate higher tree counts, but can lead to better generalization due to more gradual model updates.

• Number of Trees: Correlates with model complexity and training time. Fewer trees may underfit, while too many can overfit and slow down training.

Searching the Optimal Space

• Analytical Audit: Validate prior choices using learning curves, feature importance, and cross-validation mean square error.

• Grid Search: Exhaustively try all combinations within bounded intervals for both parameters.

Visualizing the Relationship

When executing the grid search, plotting both the learning rate and number of estimators against the chosen performance metric provides a 3D landscape view.

The Code Example

Here is the Python code:

import numpy as np
import xgboost as xgb
from sklearn.model_selection import GridSearchCV
from sklearn.datasets import load_boston, load_digits

# Load datasets
boston = load_boston()
digits = load_digits()

# Parameter grid
param_grid = {
    'learning_rate': [0.05, 0.1, 0.2, 0.3],
    'n_estimators': [50, 100, 150, 200],
}

# Grid search
clf_boston = GridSearchCV(xgb.XGBRegressor(), param_grid, cv=5, scoring='neg_mean_squared_error')
clf_digits = GridSearchCV(xgb.XGBClassifier(), param_grid, cv=5)

# Fit the models
clf_boston.fit(boston.data, boston.target)
clf_digits.fit(digits.data, digits.target)

# Best parameters
print('Best parameters for Boston:', clf_boston.best_params_)
print('Best parameters for Digits:', clf_digits.best_params_)

Early Stopping in XGBoost helps prevent overfitting and makes training more efficient by stopping iterations when performance on a validation dataset doesn’t improve. This is achieved by monitoring a metric like AUC, logloss, or error.

Implementation

1. Define Parameters: Set the parameters for early stopping:

   • eval_metric: Metric to evaluate on the validation set.
   • eval_set: Data to use for evaluation. This should be a list of tuples, with each tuple in the format (X, y). You can have multiple tuples to evaluate on multiple datasets.
   • early_stopping_rounds: The number of rounds with no improvement after which training will stop.

2. Training XGBoost Model: Train the XGBoost model with the defined parameters using xgb.train(...) or xgb.XGBClassifier.fit(...) and xgb.XGBClassifier.predict(...).

   from xgboost import XGBClassifier
   model = XGBClassifier(n_estimators=100, eval_metric='logloss', eval_set=[(X_val, y_val)], early_stopping_rounds=5)
   model.fit(X_train, y_train)
   

3. Monitoring: During training, XGBoost will evaluate the performance on the validation set after a certain number of boosting rounds, as defined by early_stopping_rounds. If the performance has not improved, training will stop.

The objective function in XGBoost plays a pivotal role in model performance optimization. It not only influences the training process but also the suitability of the model for specific tasks.

Role in Model Training

XGBoost leverages gradient boosting which focuses on optimizing the loss function at each stage. The objective function provides the form of this loss function, and the algorithm then seeks to minimize it.

• For target probabilities in binary classification, the “binary:logistic” objective uses the logarithmic loss, ensuring the model is calibrated for probabilities.
• In the “multi:softprob” objective, the loss function is defined by a distribution such as the softmax. The algorithm outputs probabilities, and the predictions can be obtained in their raw form or rounded off for class membership.

Specialized Objective Functions

Beyond covering generic use cases, XGBoost introduces specialized objective functions tailored to unique data characteristics and task requirements. For example, objective functions like “reg:logistic” suit binary classification on top of its capability to adjust for imbalanced classes.

Imperative of Customization

The flexibility to define a custom objective function is invaluable in scenarios where pre-existing ones may not suit the dataset or task optimally. This approach ensures that the model is trained on specialized loss functions most relevant to the defined problem.

Caveats of Objective Function Selection

The choice of objective function balances the interpretability of the output and the accuracy of the predictions. Models trained with different objective functions might yield disparate results and possess varying predictive traits. Therefore, selecting the most appropriate function is pivotal to optimizing model performance for desired objectives.

Code Example: Selecting an Objective Function

Here is the Python code:

import xgboost as xgb

# Define model parameters
params = {
    'objective': 'binary:logistic',  # Adjust for multi-class use cases
    'eval_metric': 'logloss'  # Use a relevant metric for validation
}

# Instantiate an XGBoost model with defined parameters
model = xgb.XGBClassifier(params=params)

# Train the model using training data
model.fit(X_train, y_train, eval_set=[(X_test, y_test)], verbose=False)

# Make predictions using the trained model
predictions = model.predict(X_test)

XGBoost is a powerful technique for addressing highly imbalanced datasets, often observed in real-world problems such as fraud detection and medical diagnosis. It offers several tools and settings optimized for imbalanced data that contribute to consistent and reliable model performance.

Key Features for Imbalanced Datasets

Weighted Loss Function

XGBoost allows for the assignment of different weights to positive and negative examples within its loss function, enabling you to counteract class imbalance.

# Example of using a weighted loss function
xgb_model = XGBClassifier(scale_pos_weight=3)

Stratified Sampling

XGBoost extends stratified sampling to each boosting round. This approach ensures that during training, a class-balanced subset of data is used to grow each new tree, thereby mitigating the issue of skewed distributions.

param['tree_method'] = 'hist'  # For improved speed
param['max_bin'] = 256  # This is the default, but it's good to be explicit
param['scale_pos_weight'] = balance_ratio

Focused Evaluation Metrics

While accuracy might not be the most reliable performance metric for imbalanced datasets, XGBoost offers a range of more nuanced measures such as F1 score, precision, and recall. Each of these can be tuned to place higher importance on either the positive or negative class.

For metric evaluation during training, set:

# Scoring metric emphasizing positive class (default is "roc_auc")
xgb_model = XGBClassifier(eval_metric='aucpr')  

Hyperparameters Optimization

For customized tuning, you can refine the behavior of XGBoost on imbalanced datasets through particular hyperparameters:

• max_delta_step: Used for batch-style predictions, it leverages thresholding to address imbalances.
• gamma (minimum loss reduction required to make a further partition): Tuning gamma can provide greater sensitivity to positive classes and improve recall.
• subsample (sample rate for each boosting round): A lower subsample rate reduces the influence of the majority class.

Tailored Features in XGBoost 1.3

The latest version of XGBoost introduced a dedicated set of functionalities to augment the handling of imbalanced data. You can reap the benefits of these updates with:

• tree_method='gpu_hist' and scale_pos_weight: Ideal for training on large GPUs
• enable_experimental_json: true for flexible interaction with Bolt inspired JSON interface.